Recurrent problem

Actuarial work involves calculating the present value of future liabilities.  In the case of pension funds and annuity portfolios, this means valuing future pension payments. This typically involves calculating a lot of annuity factors, often using spreadsheets.

One approach is to calculate the survival curve, then to apply a discount factor to calculate the present value of payments at each age.  Summing these discounted future values gives the annuity factor at the outset age of the survival curve.  However, if annuity factors have to be calculated en masse, it is sometimes much more effective to make use of the recurrence relations between successive annuity factors, as shown in Figure 1.

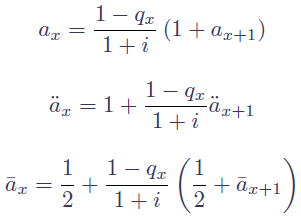
where i is the interest rate and q_x is the mortality rate at age x.  These recurrence relations are particularly useful when having to calculate an annuity factor which includes allowance for benefits paid to a surviving spouse.  For this we need not only the single-life annuity factors for the first and second life, but also the factor for a joint-life annuity, i.e. one which terminates on the first death.  These are shown in Figure 2:

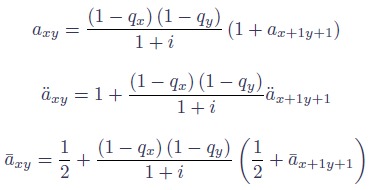
where y is the spouse's age. Finally, we just need the formulae for calculating annuity factors where f is the proportion of the main benefit paid to the spouse after death of the main life, as shown in Figure 3:

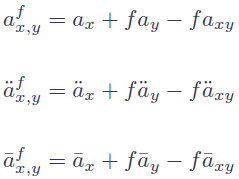
The recurrence relations in Figure 1, 2 and 3 can be very useful when one has to calculate a large number of annuity factors, and they are especially useful when spouses' benefits are involved.