Fifteen-year (h)itch

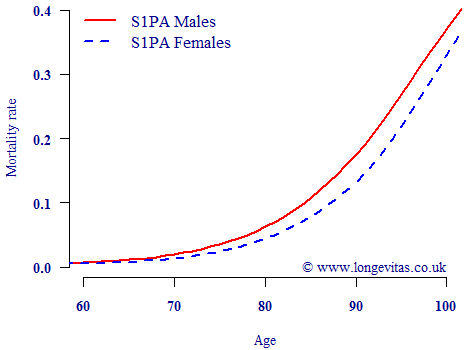
Effective risk modelling is about grouping people with shared characteristics which affect this risk.  In mortality analysis by far the most important risk factor is age, so it is not a good idea to mix the young and old if it can be avoided.  By way of illustration, Figure 1 shows that mortality rates increase exponentially over much of the post-retirement age range. 

Figure 1. Mortality rates for males and females according to table S1PA from the CMI. The exponential rise in mortality rates means it is important not to mix ages which are too far apart.

Despite the steep rise in risk by age, it was relatively common until the late 1990s to use five-year age ranges for mortality models.  This was a deliberate trade-off between making calculations simpler, but also trying to minimise the errors inherent in grouping people of radically different risk levels.  However, with the advent of much greater computing power, actuaries no longer need to make such compromises in mortality modelling.

We were therefore surprised recently when we came across a commercial mortality tool for pensioners which contained rating factors applied to fifteen-year age ranges.  The width of these ranges could be a major problem: the mortality rate for males aged 79 according to the S1PA table from the CMI is almost five times the rate at age 65.  When working with grouped ages, the worry is that the age distribution of the data set used to calibrate a tool is not the same as the portfolio being rated or analysed.  The wider the age range, the greater this source of error is.

Ideally, of course, the age range is kept as narrow as possible to minimise such errors.  However, with the advent of survival models it has been possible to eliminate this source of error altogether.  By using exact ages calculated at the level of the individual, mortality analysis using survival models effectively has an age range of one day.