Dealing direct

Data in Longevitas takes two forms. Firstly, we have the user-uploaded data, which has normally been extracted from an administration system with only modest formatting and then secondly, we have operation input data which is the bare-bones format necessary to support a specific calculation. The system knows how to generate input data from user-uploaded data, but the process is strictly one-way. The input data does not contain sufficient information to be able to reconstitute the original records.

All of our operations have their own structure for input data, but all share a focus on brevity and suitability for the task in hand. As a result of this, all personally identifiable details are excised from operation input format; for example in modelling, names and postcodes that are optionally uploaded for the deduplication and profiling stages are no longer present. Here is a fragment of survival model input data, where the LongevitasId field allows you to tie back to the originally uploaded records:

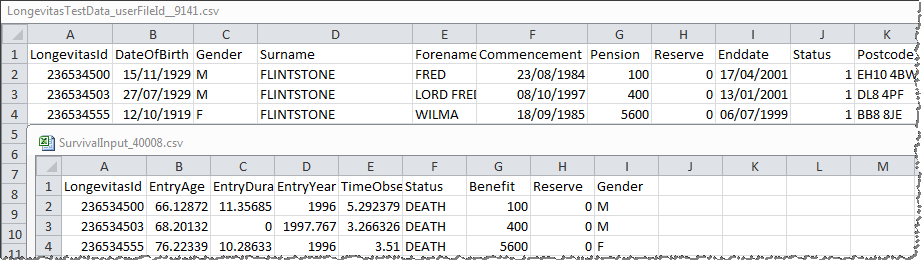
Note in the example above that dates have been turned into terms and ages corresponding to model boundaries and settings which are not themselves visible in the dataset. All the exposure calculation rules used in this transformation are fully documented in our technical guide, and of course, the input data is available to access after the operation is complete. This openness is important to us – when a model is run, we want you to be able to take this input data away and perform your own testing or analysis in any tool you choose. There is an example of doing just this with R at the end of our Longevitas application walkthrough.

Since we are discussing the fundamental data required by modelling, a further key aspect of this is that data can be supplied this way in the first place. You can supplement the data from an uploaded file using your choice of dataset(s) in direct input format, and you can even model solely against direct input data. This provides some interesting capabilities, both to (a) enrich a model against a smaller dataset with direct input data from a larger and more powerful one or, (b) to operate against completely anonymised data prepared in-house. It may not be as straightforward as the standard ways of working, but it is nice to have options.