The actuarial data onion

Actuaries tasked with analysing a portfolio's mortality experience face a gap between what has happened in the outside world and the data they actually work with.  The various difference levels are depicted in Figure 1.

Figure 1.  The actuarial data onion.

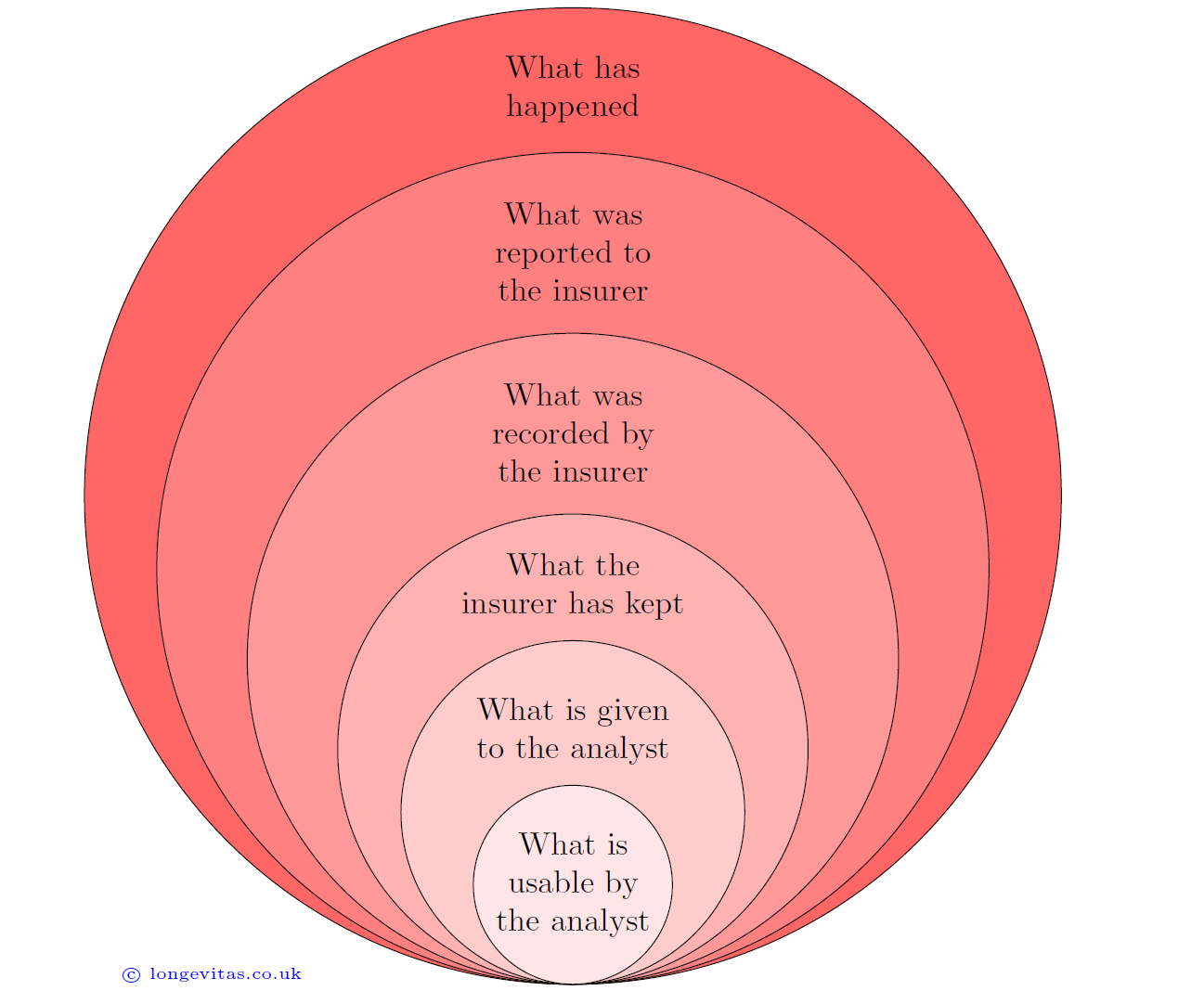
The first difference is between what has happened in the outside world and what has been reported to the insurer. In the case of mortality, there is usually a reporting delay. The impact and extent of these late-reported deaths varies by insurer (Richards, 2022). A simple solution is to discard the most recent experience data, but there exist methods to allow for occurred-but-not-reported (OBNR) deaths to make full use of all available data.

The next potential difference lies in what the insurer actually records.  In Richards et al (2013) only the year of death was actually recorded by the administrator.  Furthermore, annuities that commenced and terminated in the same calendar year did not appear at all in the annual data extracts.

Another problem is that what is recorded can subsequently be lost or even actively deleted.  When a pension scheme changes third-party administrator, for example, details of past deaths are seldom migrated and are thus lost.  Even without a system migration, some IT departments will delete past death records, despite this information having considerable business value.

The next difference lies in what is made available to the analyst.  Privacy concerns are often cited when mortality experience data has to go outside an organization, say when inviting reinsurers to bid for a longevity swap.  However, ceding organizations need to be aware that withholding names and postcodes can lead to higher prices due to the bidder's inability to  deduplicate or use geodemographic profiling.  Interestingly, in some organizations it is becoming difficult for even internal analysts to get hold of such data for their day-to-day work.

Lastly, there is the question of what parts of the supplied data an analyst can actually use.  If the analyst is using traditional actuarial models based around \(q_x\), then parts of the data will have to be discarded to fit the model's requirement for integer years of exposure.  However, modern methods use survival models based around the mortality hazard rate, \(\mu_x\), which do not require data to be discarded.

As with peeling a real onion, the various layers of deletion, degradation or denial are enough to make an actuary weep.  To avoid further tears, the actuary also needs to be wary that no bias is introduced.  However, at least there is no need to add to these woes by discarding data just because it is inconvenient for a model based on \(q_x\).  Fortunately, actuaries can make use of every scrap of available data by using survival models for \(\mu_x\).