The strange case of Scotland's missing improvements

Earlier this week I had the opportunity to attend a New Scientist: Live presentation given by Sir Harry Burns entitled "Making Scotland Well Again", which was an examination of the links between social conditions and incidence of disease. We've written about mortality in Scotland before, but from his diverse roles including consultant surgeon, Glasgow's director of public health and former Chief Medical Officer for Scotland, Harry Burns has unique insight into the matter.

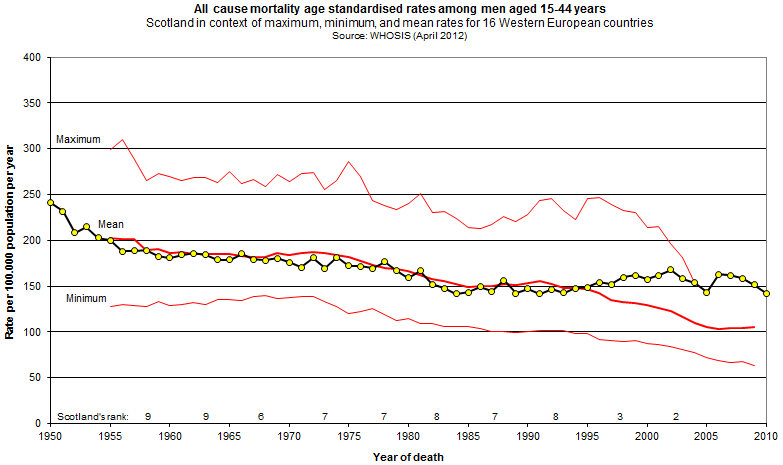
A core aspect of the situation for Burns is its relative recency. He reflected upon the fact that Scottish life expectancy sat around the Western European average until just after World War II. After that time, Scottish mortality simply didn't improve fast enough to avoid the country being labelled the sick man of Europe.

So, why did a proportion of Scotland's post-war improvements go AWOL? Burns was at pains to make clear it isn't explained by significantly worse diet, obesity, hypertension or higher rates of smoking. It isn't explained by deprivation either, since in a UK context, Glasgow's deprivation profile matches that of comparable cities in the North of England. In fact, around 60% of Scotland's excess mortality stems from psycho-social causes: alcohol, drugs, violence and suicide. The remaining excess is mainly attributable to cancer, cardiovascular causes and stroke. The psycho-social impacts play out predominantly amongst younger people, and the effect of this is shown starkly in the following chart from the GCPH, comparing younger mortality to the Western European average.

Sir Harry believes the underlying jigsaw-puzzle is now more-or-less complete. Social conditions, such as those arising from the deindustrialisation of west-central Scotland since the 1950's, have had profound effects. Chaotic early lives, stemming often from parental substance abuse and domestic violence, result not only in psychological problems, but also physical changes in developing brain structures. This produces brains that prioritise survival and the cortisol-fuelled readiness for fight-or-flight over the development of higher-order processes. Even small differences in the stress hormone cortisol, by mobilising fats in the blood for ready energy, will over decades exacerbate atherosclerotic and inflammatory impacts. Many of these effects now appear to be epigenetically heritable, passing from one generation to the next.

But why don't we see near-identical severity of impacts in Manchester or Liverpool? For Burns, the answer lies in two specific areas. Firstly by replacing traditional Victorian tenements with problematic alternatives such as high-density tower blocks, of which Glasgow contained the highest concentration in the UK, vital community support structures were lost. This acted in concert with the personality differences found by the three-city survey research project and Burns suggested these findings may be underscored by a more recent commercial study. Essentially, the picture is one where lower levels of trust and social cohesion left west-central Scotland markedly more vulnerable to the pressures of poverty.

As you might expect, a currently serving Professor of Global Public Health would not simply outline a problem without also proposing a solution. One message he took to the Scottish Government was: "Invest in early years. We won't see immediate results, but in 40 years we'll be closing prisons.". And, by extension, hopefully reducing pressure on Scotland's health services as well. Creating targeted initiatives is a complex business, and success is never guaranteed, but were public health efforts such as these to bear fruit perhaps we can one day leave our "sick man" mantle behind and happily reclaim our position as Mr (or Ms.) Distinctly Average.